حل معادلات دیفرانسیل با شرایط مرزی در متلب
چنانچه در قبلا اشاره کردیم در متلب مشتق مرتبه اول یعنی dy/dx بصورت Dy و مشتق مرتبه دوم بصورت D2y و ... نوشته میشود.مثلا برای حل معادله دیفرانسیل زیر:
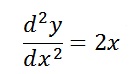
با شرایط مرزی:

برنامه را بصورت زیر مینویسیم:

چنانچه در قبلا اشاره کردیم در متلب مشتق مرتبه اول یعنی dy/dx بصورت Dy و مشتق مرتبه دوم بصورت D2y و ... نوشته میشود.مثلا برای حل معادله دیفرانسیل زیر:
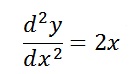
با شرایط مرزی:

برنامه را بصورت زیر مینویسیم:

در متلب مشتق مرتبه اول یعنی dy/dx بصورت Dy و مشتق مرتبه دوم بصورت D2y و ... نوشته میشود.مثلا برای حل معادله دیفرانسیل زیر:
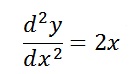
از برنامه زیر استفاده میکنیم:

پس از اجرا جواب بصورت زیر به نمایش درخواهد آمد:
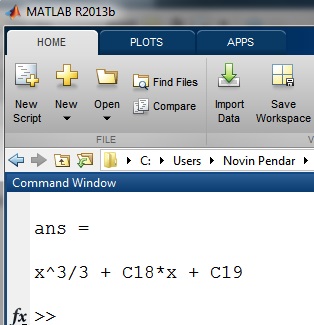
که در آن C18 و C19 ضرایب ثابتی هستند که با مشخص شدن شرایط اولیه بدست میآیند.
وقتی میخواهیم تابع f(x) را در فاصله بین a و b رسم کنیم باید در برنامه شکل تابع را در سطر دهم بنویسیم. اگر هدف رسم sin(x) باشد، آن را در سطر دهم مینویسیم. برنامه را اجرا میکنیم. هنگام اجرا برنامه نقطه شروع یعنی a و نقطه خاتمه یعنی b و همچنین تعداد تقسیمات یعنی N را از ما میخواهد و سپس تابع در صفحه figure بطور پیوسته رسم میشود. در زیر برنامه مربوطه آمده است:
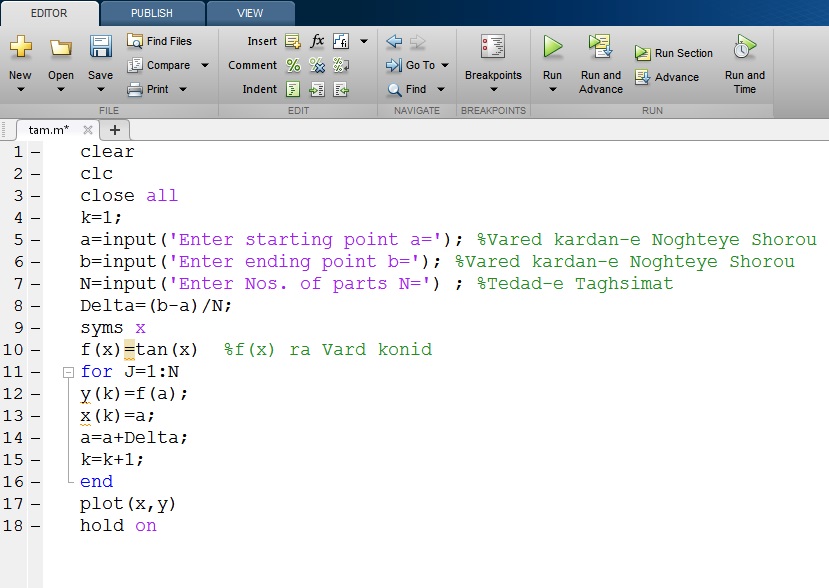
اکنون قصد داریم انتگرال معین زیر را به روش ذوزنقهای حل کنیم:

در x=0 انتگرالده یعنی f(0) تعریف نشده است. از این رو در برنامه نویسی مقدار حد آن را وقتی که x به سمت 0 میل میکند؛ قرار میدهیم. یعنی همانند عبارت داخل کادر قرمز قرار میدهیم:
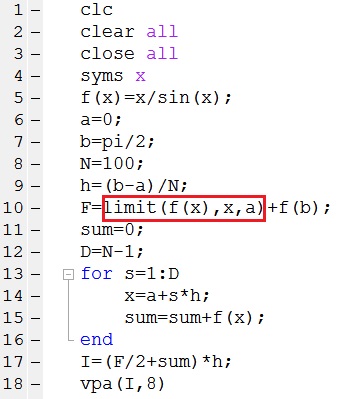
دستور vpa(I,8) به ما کمک میکند تا حاصل را تا دقت 8 رقم معنیدار بدست آوریم
نگارش: ابوالفضل باباپور خاروانا
در نرم افزار متلب (Matlab)، انتگرال معین هر تابع را می توان با دستور trapz(x,y) و با روش های عددی محاسبه کرد. در دستور فوق x , y دو بردار هستند که مقادیر متغیر مستقل و تابع را در خود جای داده اند. در این دستور هرچه رزولوشن یا تعداد نقاط بردارهای x , y بیشتر باشد نتیجه انتگرال دقیق تر است. در این مثال فاصله بین صفر و عدد پی به 100 قسمت تقسیم شده است. جهت حل انتگرال زیر:

مطابق شکل بالا؛ برنامه را در Command Window مینویسیم و اجرا میکنیم. میتوانیم برنامه را Editor هم بصورت زیر بنویسیم و اجرا کنیم:
x=linspace(0,pi,100)
y=sin(x)
trapz(x,y)
ملاحظه میشود که بجای جواب دقیق آن که 2 هست، جواب 1.9998 بدست میآید.چنانچه اشاره شد هر چقدر تعداد تقسیمات بیشتر باشد، جواب انتگرال دقیقتر بدست میآید.