اکنون قصد داریم انتگرال معین زیر را به روش ذوزنقه‌ای حل کنیم:
در x=0 انتگرال‌ده یعنی f(0) تعریف نشده است. از این رو در برنامه نویسی مقدار حد آن را وقتی که x به سمت 0 میل می‌کند؛ قرار می‌دهیم. یعنی همانند عبارت داخل کادر قرمز قرار می‌دهیم:
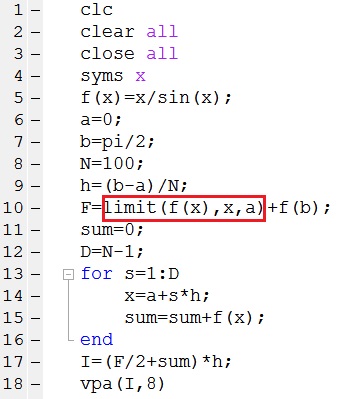
دستور vpa(I,8) به ما کمک می‌کند تا حاصل را تا دقت 8 رقم معنی‌دار بدست آوریم
نگارش: ابوالفضل باباپور خاروانا
در نرم افزار متلب (Matlab)، انتگرال معین هر تابع را می توان با دستور trapz(x,y) و با روش های عددی محاسبه کرد. در دستور فوق x , y دو بردار هستند که مقادیر متغیر مستقل و تابع را در خود جای داده اند. در این دستور هرچه رزولوشن یا تعداد نقاط بردارهای x , y بیشتر باشد نتیجه انتگرال دقیق تر است. در این مثال فاصله بین صفر و عدد پی به 100 قسمت تقسیم شده است. جهت حل انتگرال زیر:
مطابق شکل بالا؛ برنامه را در Command Window می‌نویسیم و اجرا می‌کنیم. می‌توانیم برنامه را Editor هم بصورت زیر بنویسیم و اجرا کنیم:
x=linspace(0,pi,100)
y=sin(x)
trapz(x,y)
ملاحظه می‌شود که بجای جواب دقیق آن که 2 هست، جواب 1.9998 بدست می‌آید.چنانچه اشاره شد هر چقدر تعداد تقسیمات بیشتر باشد، جواب انتگرال دقیق‌تر بدست می‌آید.
امروزه پروژه چند ملیتی ایتر ، نانو تکنولوژی ، شتابدهنده هادرون ، شاتل آنلانتیس و ... توانایی منحصر به فرد و انکار ناپذیر فیزیک کاربردی ، فیزیک نظری و فیزیک محاسباتی را بخوبی نمایش می‌دهند.انشتین بزرگ در باره توانایی فیزیک فرموده است :